Recent research has challenged the widespread belief that gender inequities in academia would disappear simply by increasing the number of women. More complex causes might be at play, embodied in the networked structure of scientific collaborations. Here, we aim to understand the structural inequality between male and female scholars in the dissemination of scientific knowledge. We use a large-scale dataset of academic publications from the American Physical Society (APS) to build a time-varying network of collaborations from 1970 to 2020. We model knowledge dissemination as a contagion process in which scientists become informed based on the propagation of knowledge through their collaborators. We quantify the fairness of the system in terms of how women acquire and diffuse knowledge compared to men. Our results indicate that knowledge acquisition and diffusion are slower for women than expected. We find that the main determinant of women’s disadvantage is the gap in the cumulative number of collaborators, highlighting how time creates structural disadvantages that contribute to marginalize women in physics. Our work sheds light on how the dynamics of scientific collaborations shape gender disparities in knowledge dissemination and calls for a deeper understanding on how to intervene to improve fairness and diversity in the scientific community.

The most fundamental social interactions among humans occur face to face. Their features have been extensively studied in recent years, owing to the availability of high-resolution data on individuals’ proximity. Mathematical models based on mobile agents have been crucial to understand the spatio-temporal organization of face-to-face interactions. However, these models focus on dyadic relationships only, failing to characterize interactions in larger groups of individuals. Here, we propose a model in which agents interact with each other by forming groups of different sizes. Each group has a degree of social attractiveness, based on which neighboring agents decide whether to join. Our framework reproduces different properties of groups in face-to-face interactions, including their distribution, the correlation in their number, and their persistence in time, which cannot be replicated by dyadic models. Furthermore, it captures homophilic patterns at the level of higher-order interactions, going beyond standard pairwise approaches. Our work sheds light on the higher-order mechanisms at the heart of human face-to-face interactions, paving the way for further investigation of how group dynamics at a microscopic scale affects social phenomena at a macroscopic scale.

Many real-world complex systems are characterized by interactions in groups that change in time. Current temporal network approaches, however, are unable to describe group dynamics, as they are based on pairwise interactions only. Here, we use time-varying hypergraphs to describe such systems, and we introduce a framework based on higher-order correlations to characterize their temporal organization. The analysis of human interaction data reveals the existence of coherent and interdependent mesoscopic structures, thus capturing aggregation, fragmentation and nucleation processes in social systems. We introduce a model of temporal hypergraphs with non-Markovian group interactions, which reveals complex memory as a fundamental mechanism underlying the emerging pattern in the data.

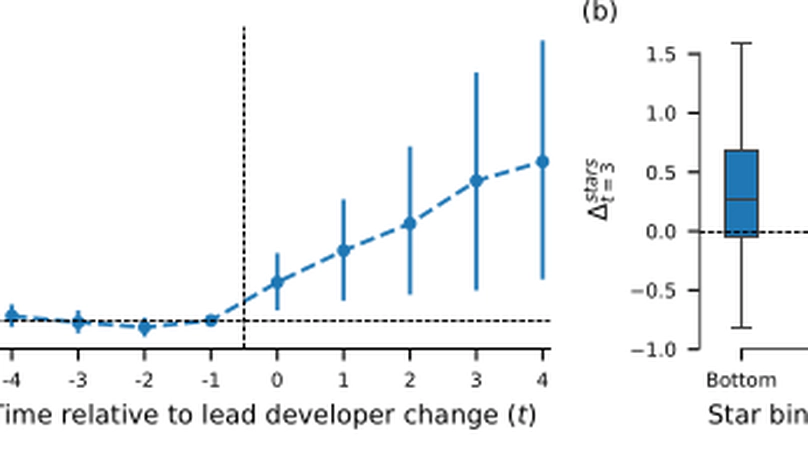
From science to industry, teamwork plays a crucial role in knowledge production and innovation. Most studies consider teams as static groups of individuals, thereby failing to capture how the micro-dynamics of collaborative processes and organizational changes determine team success. Here, we leverage fine-grained temporal data on software development teams to gain insights into the dynamics of online collaborative projects. Our analysis reveals an uneven workload distribution in teams, with stronger heterogeneity correlated with higher success, and the early emergence of a lead developer carrying out the majority of work. Moreover, we find that a sizeable fraction of projects experience a change of lead developer, with such a transition being more likely in projects led by inexperienced users. Finally, we show that leadership change is associated with faster success growth, in particular for the least successful projects. Our work contributes to a deeper understanding of the link between team evolution and success in collaborative processes.