Abstract
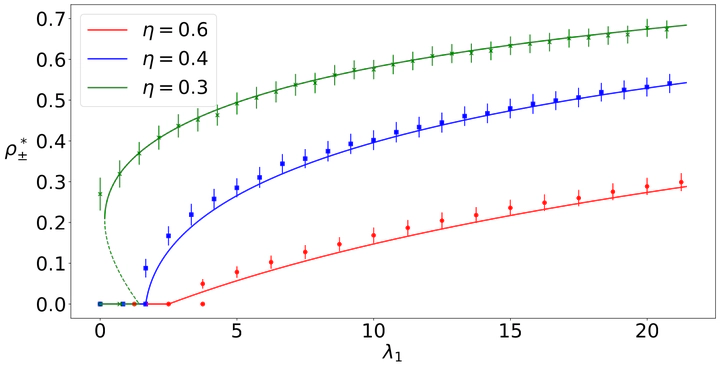
Social systems are characterized by the presence of group interactions and by the existence of both trust and distrust relations. Although there is a wide literature on signed social networks, where positive signs associated to the links indicate trust, friendship, agreement, while negative signs represent distrust, antagonism, and disagreement, very little is known about the effect that signed interactions can have on the spreading of social behaviors when higher-order interactions are taken into account. In this paper we focus on processes of complex contagion, such as the adoption of social norms, where exposure to multiple sources is needed for the contagion to occur. Complex contagion has been recently modeled by higher-order networks, such as simplicial complexes, which allow transmission to happen not only through the links connecting pair of nodes, but also in group interactions, namely over simplices of dimension larger or equal than two. Here, we introduce a model of complex contagion on signed simplicial complexes, and we investigate the role played by trust and distrust on the dynamics of a social contagion process. The presence of higher-order signed structures in our model naturally induces new infection and recovery mechanisms. Through numerical simulations and analytical results in the mean-field approximation, we show how distrust determines the way the system moves from a state where no individuals adopt the social behavior, to a state where a finite fraction of the population actively spreads it. Interestingly, the fraction of spreading individuals displays a non-monotonic dependence on the average number of connections between individuals. We then investigate how social balance affects social contagion, finding that balanced triads either promote or impede contagion based on the relative abundance of fully trusted relations.
Luca Gallo
Postdoctoral research fellow
My research focuses on applying network science to studying the structure and dynamics of social systems.