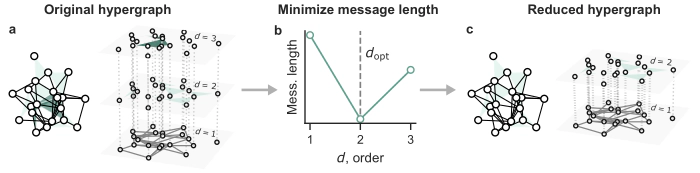
Abstract
Empirical complex systems are widely assumed to be characterized not only by pairwise interactions, but also by higher-order (group) interactions that affect collective phenomena, from metabolic reactions to epidemics. Nevertheless, higher-order networks’ superior descriptive power – compared to classical pairwise networks – comes with a much increased model complexity and computational cost. Consequently, it is of paramount importance to establish a quantitative method to determine when such a modeling framework is advantageous with respect to pairwise models, and to which extent it provides a parsimonious description of empirical systems. Here, we propose a principled method, based on information compression, to analyze the reducibility of higher-order networks to lower-order interactions, by identifying redundancies in diffusion processes while preserving the relevant functional information. The analysis of a broad spectrum of empirical systems shows that, although some networks contain non-compressible group interactions, others can be effectively approximated by lower-order interactions – some technological and biological systems even just by pairwise interactions. More generally, our findings mark a significant step towards minimizing the dimensionality of models for complex systems.
Luca Gallo
Postdoctoral research fellow
My research focuses on applying network science to studying the structure and dynamics of social systems.